Logistic regression for musical tags

by Marianne de Heer Kloots & Ashley Burgoyne, September 2022

Welcome to your first ANCM lab! This session focusses on how logistic models can be useful not just as discrete classifiers but also as a means to develop an interpretable continuous measurement. Your goal is not to develop the best classifier per se, but rather to develop a continuous measure that you can explain. Your deliverable for the final portfolio will be a short description of your model, your measurement, and a qualitative description (based on your own listening) of how well your measurement seems to capture a musical concept (250–500 words).

What kind of musical concept? The lab works with a widely-used dataset in music information retrieval (MIR) known as the MagnaTagATune dataset. This dataset is normally used for its clean and consensus-based collection of ‘tags’ that participants in an online experiment chose to associate with 31 000 clips of open-source music from the Magnatune collection.

You may be familiar with the concept of a music tag from the last.fm service. In brief, a tag it is any user-defined label that a listener chooses associate with a track they are hearing. Tags can be highly personal and specific (e.g., dark rainy city), but as researchers, we are most interested in tags that many different listeners independently chose to associate with a track. The key advantage of tags over marketing-driven categories like genre, which are ultimately oriented more toward predicting sales or streams than the audio content itself, is that tags can be a better representation of listeners’ conceptualisation of the music that they hear.

import numpy as np
import pandas as pd
import os
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold, GridSearchCV
from IPython.display import Audio
from IPython.display import display

Loading the data

We will work with a set of features computed by a convolutional neural network model (specifically the TUNe+ architecture, which expand the widely used U-Net architecture), trained to learn a self-supervised music representation from audio. You will learn more about these architectures next week, but if you would like to read more about the specifics of the model already, read the Vélez Vázquez and Burgoyne 2022 preprint on Canvas.

For this lab, however, all you need to know about the TUNe+ representation is that it consists of a 512-dimensional extracted feature vector for each of the 25.000+ audio clips in MagnaTagATune. Self-supervised networks learn without reference to any specific task or ground truth, and so in principle, it is an open question whether the TUNe+ representation has learned anything useful for music tagging. Your job is to find a feature (or set of features) in this representation that seem to generate a good prediction of one or more of the MagnaTagATune tags.

To load the features into your colab environment, go here and click add shortcut to drive (plus symbol in the top right): tune_plus.zip

Then link your google drive to colab (run the code cell below):

from google.colab import drive
drive.mount('/content/drive')

Mounted at /content/drive

Unzip the files into a folder (you will be able to find this folder if you click the folder icon in your left sidebar):

!unzip -qq '/content/drive/MyDrive/tune_plus.zip'

Now we download the tag annotations from the MagnaTagATune dataset.

!wget -q 'https://mirg.city.ac.uk/datasets/magnatagatune/annotations_final.csv'

We load both the features and annotations into separate pandas DataFrames. Have a look at the content of the dataframes below.

features_dir = 'tune_plus/'
annotations_df = pd.read_csv('annotations_final.csv', sep='\t')

# remove three missing clips from the annotations dataframe
missing_clips = [clip_id for clip_id in annotations_df['clip_id'] if not os.path.exists(features_dir + str(clip_id).zfill(5) + '.npy')]
annotations_df = annotations_df.drop(annotations_df[annotations_df['clip_id'].isin(missing_clips)].index)

# standardise the features and use the clip_ids as row names
annotations_df = annotations_df.set_index('clip_id')
raw_features_df = pd.DataFrame.from_dict({clip_id: np.load(features_dir + str(clip_id).zfill(5) + '.npy') 
                                         for clip_id in annotations_df.index}, orient='index')
features_df = pd.DataFrame(StandardScaler().fit_transform(raw_features_df))
features_df.index = raw_features_df.index
features_df.index.name = 'clip_id'

# row names are clip_id, last column is the mp3 file location, all other columns are binary 1/0 annotations for each tag
annotations_df

	no voice	singer	duet	plucking	hard rock	world	bongos	harpsichord	female singing	clasical	...	rap	metal	hip hop	quick	water	baroque	women	fiddle	english	mp3_path
clip_id
2	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	f/american_bach_soloists-j_s__bach_solo_cantat...
6	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	1	0	0	0	f/american_bach_soloists-j_s__bach_solo_cantat...
10	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	f/american_bach_soloists-j_s__bach_solo_cantat...
11	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	f/american_bach_soloists-j_s__bach_solo_cantat...
12	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	f/american_bach_soloists-j_s__bach_solo_cantat...
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
58899	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	8/jacob_heringman-blame_not_my_lute-56-la_bres...
58906	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	8/jacob_heringman-blame_not_my_lute-57-lost_is...
58907	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	8/jacob_heringman-blame_not_my_lute-57-lost_is...
58908	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	8/jacob_heringman-blame_not_my_lute-57-lost_is...
58915	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	8/jacob_heringman-blame_not_my_lute-58-a_toy_f...

25860 rows × 189 columns

# all_tags contains all tags present in the MagnaTagATune annotations (all columns except for mp3_path)
all_tags = [col for col in annotations_df.columns if col != 'mp3_path']
print(all_tags)

['no voice', 'singer', 'duet', 'plucking', 'hard rock', 'world', 'bongos', 'harpsichord', 'female singing', 'clasical', 'sitar', 'chorus', 'female opera', 'male vocal', 'vocals', 'clarinet', 'heavy', 'silence', 'beats', 'men', 'woodwind', 'funky', 'no strings', 'chimes', 'foreign', 'no piano', 'horns', 'classical', 'female', 'no voices', 'soft rock', 'eerie', 'spacey', 'jazz', 'guitar', 'quiet', 'no beat', 'banjo', 'electric', 'solo', 'violins', 'folk', 'female voice', 'wind', 'happy', 'ambient', 'new age', 'synth', 'funk', 'no singing', 'middle eastern', 'trumpet', 'percussion', 'drum', 'airy', 'voice', 'repetitive', 'birds', 'space', 'strings', 'bass', 'harpsicord', 'medieval', 'male voice', 'girl', 'keyboard', 'acoustic', 'loud', 'classic', 'string', 'drums', 'electronic', 'not classical', 'chanting', 'no violin', 'not rock', 'no guitar', 'organ', 'no vocal', 'talking', 'choral', 'weird', 'opera', 'soprano', 'fast', 'acoustic guitar', 'electric guitar', 'male singer', 'man singing', 'classical guitar', 'country', 'violin', 'electro', 'reggae', 'tribal', 'dark', 'male opera', 'no vocals', 'irish', 'electronica', 'horn', 'operatic', 'arabic', 'lol', 'low', 'instrumental', 'trance', 'chant', 'strange', 'drone', 'synthesizer', 'heavy metal', 'modern', 'disco', 'bells', 'man', 'deep', 'fast beat', 'industrial', 'hard', 'harp', 'no flute', 'jungle', 'pop', 'lute', 'female vocal', 'oboe', 'mellow', 'orchestral', 'viola', 'light', 'echo', 'piano', 'celtic', 'male vocals', 'orchestra', 'eastern', 'old', 'flutes', 'punk', 'spanish', 'sad', 'sax', 'slow', 'male', 'blues', 'vocal', 'indian', 'no singer', 'scary', 'india', 'woman', 'woman singing', 'rock', 'dance', 'piano solo', 'guitars', 'no drums', 'jazzy', 'singing', 'cello', 'calm', 'female vocals', 'voices', 'different', 'techno', 'clapping', 'house', 'monks', 'flute', 'not opera', 'not english', 'oriental', 'beat', 'upbeat', 'soft', 'noise', 'choir', 'female singer', 'rap', 'metal', 'hip hop', 'quick', 'water', 'baroque', 'women', 'fiddle', 'english']

# row names are clip_id, column names are feature index
# features_df
features_df

	0	1	2	3	4	5	6	7	8	9	...	502	503	504	505	506	507	508	509	510	511
clip_id
2	-0.378277	-0.062457	-0.510482	-0.480929	-0.480325	-0.454518	-0.443122	-0.493741	-0.213347	2.126731	...	-0.291182	-0.466146	0.551430	1.003683	-0.113972	-0.421089	-0.255160	-0.354635	-0.050093	-0.389713
6	-0.376851	0.296082	-0.484719	-0.480929	-0.433477	-0.352741	-0.486704	-0.493741	0.150385	2.665289	...	-0.291182	-0.466146	0.307409	1.013029	-0.070639	-0.421089	0.257779	-0.327240	-0.386583	-0.388235
10	-0.461711	-0.052404	-0.461220	-0.480929	-0.561454	-0.300693	-0.524904	-0.435769	-0.172081	2.452786	...	-0.291182	-0.466146	0.527835	1.004471	0.130523	-0.421089	-0.177004	-0.354635	-0.345239	-0.056744
11	-0.448789	-0.379482	-0.510482	-0.470660	-0.453445	-0.536019	-0.524904	-0.277493	-0.388461	1.073273	...	-0.291182	-0.466146	0.566224	0.950023	-0.205476	-0.406373	0.466494	-0.352163	-0.084332	-0.320166
12	-0.440095	-0.405996	-0.504078	-0.480929	-0.441189	-0.436168	-0.524904	-0.299977	-0.217573	1.405112	...	-0.291182	-0.466146	0.451640	0.815182	0.495791	-0.421089	0.842923	-0.332279	-0.349359	-0.360313
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
58899	-0.461711	-0.405996	-0.510482	-0.480929	-0.609133	-0.560925	0.547899	-0.449088	-0.542852	-0.504916	...	-0.134670	-0.466146	-0.565874	-0.399633	-0.564821	2.098686	-0.371062	-0.118584	-0.463082	-0.389713
58906	-0.461711	-0.349007	-0.510482	-0.480929	-0.609133	-0.533283	-0.355478	-0.459859	-0.552699	-0.537892	...	-0.291182	-0.466146	-0.566145	-0.517899	-0.564821	4.606868	-0.371062	-0.321390	-0.463082	-0.389713
58907	-0.461711	-0.405996	-0.510482	-0.440443	-0.609133	-0.504413	-0.044520	-0.380819	-0.552699	-0.537892	...	-0.291182	-0.461540	-0.573039	-0.434897	-0.564821	4.504693	-0.371062	-0.354635	-0.463082	-0.389713
58908	-0.461711	-0.405996	-0.510482	-0.430805	-0.599298	-0.560925	-0.284452	-0.449022	-0.552699	-0.537892	...	-0.291182	-0.461882	-0.573039	-0.517899	-0.564821	2.294687	-0.371062	-0.354635	-0.463082	-0.389713
58915	-0.461711	-0.369697	-0.510482	-0.480929	-0.609133	-0.560925	0.744182	-0.493741	-0.552699	-0.537892	...	-0.291182	-0.466146	-0.562144	-0.400010	-0.564821	1.812065	-0.371062	-0.217233	-0.463082	-0.389713

25860 rows × 512 columns

Each clip has a unique clip_id, used as the row names in both dataframes. This is how we know which features, tag annotations and mp3 files belong to eachother. In annotations_df, you can get the 0/1 values of a particular tag like ‘harpsichord’ for all clips using the column names: annotations_df['harpsichord']. In features_df, you can similarly use the columns to get the values of a single feature (like the 204th one out of 512) using features_df[203] (remember Python is zero-indexed).

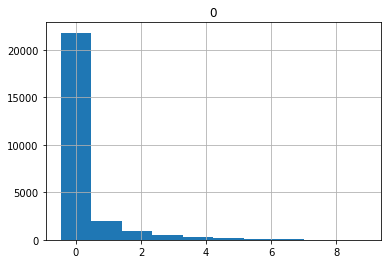
Note that even though we standardised the feature values, they are not at all bell shaped! All of the features have a mode just below 0 with a long right tail. Here is histogram of feature 0, for example.

features_df.hist(0)

array([[<matplotlib.axes._subplots.AxesSubplot object at 0x7f9afe173c10>]],
      dtype=object)

Let’s also load the actual mp3 files so we can listen to some clips. We need to add a shortcut to your Google drive again, but now for the following zip file: mp3.zip. Then also unzip this one into a folder:

!unzip -qq '/content/drive/MyDrive/mp3.zip'

Now you can listen to the audio for any clip_id you’d like (enjoy!):

my_clip = 58907
sound_file = annotations_df.loc[my_clip, 'mp3_path']
sound_audio = Audio(sound_file) 
display(sound_audio)

Here’s a quick function to find the positive tag annotations (all columns that have a 1) for any clip_id.

def get_tags(clip_id):
  return [col for col in annotations_df.columns if annotations_df.loc[clip_id, col] == 1]

tags_for_my_clip = get_tags(my_clip)
print(tags_for_my_clip)

['classical', 'guitar', 'strings', 'slow']

Do you agree?

(Below are all tags not chosen – or at least not chosen by many people – for this particular clip.)

print([tag for tag in all_tags if not tag in tags_for_my_clip])

['no voice', 'singer', 'duet', 'plucking', 'hard rock', 'world', 'bongos', 'harpsichord', 'female singing', 'clasical', 'sitar', 'chorus', 'female opera', 'male vocal', 'vocals', 'clarinet', 'heavy', 'silence', 'beats', 'men', 'woodwind', 'funky', 'no strings', 'chimes', 'foreign', 'no piano', 'horns', 'female', 'no voices', 'soft rock', 'eerie', 'spacey', 'jazz', 'quiet', 'no beat', 'banjo', 'electric', 'solo', 'violins', 'folk', 'female voice', 'wind', 'happy', 'ambient', 'new age', 'synth', 'funk', 'no singing', 'middle eastern', 'trumpet', 'percussion', 'drum', 'airy', 'voice', 'repetitive', 'birds', 'space', 'bass', 'harpsicord', 'medieval', 'male voice', 'girl', 'keyboard', 'acoustic', 'loud', 'classic', 'string', 'drums', 'electronic', 'not classical', 'chanting', 'no violin', 'not rock', 'no guitar', 'organ', 'no vocal', 'talking', 'choral', 'weird', 'opera', 'soprano', 'fast', 'acoustic guitar', 'electric guitar', 'male singer', 'man singing', 'classical guitar', 'country', 'violin', 'electro', 'reggae', 'tribal', 'dark', 'male opera', 'no vocals', 'irish', 'electronica', 'horn', 'operatic', 'arabic', 'lol', 'low', 'instrumental', 'trance', 'chant', 'strange', 'drone', 'synthesizer', 'heavy metal', 'modern', 'disco', 'bells', 'man', 'deep', 'fast beat', 'industrial', 'hard', 'harp', 'no flute', 'jungle', 'pop', 'lute', 'female vocal', 'oboe', 'mellow', 'orchestral', 'viola', 'light', 'echo', 'piano', 'celtic', 'male vocals', 'orchestra', 'eastern', 'old', 'flutes', 'punk', 'spanish', 'sad', 'sax', 'male', 'blues', 'vocal', 'indian', 'no singer', 'scary', 'india', 'woman', 'woman singing', 'rock', 'dance', 'piano solo', 'guitars', 'no drums', 'jazzy', 'singing', 'cello', 'calm', 'female vocals', 'voices', 'different', 'techno', 'clapping', 'house', 'monks', 'flute', 'not opera', 'not english', 'oriental', 'beat', 'upbeat', 'soft', 'noise', 'choir', 'female singer', 'rap', 'metal', 'hip hop', 'quick', 'water', 'baroque', 'women', 'fiddle', 'english']

Logistic regression

Using the popular sklearn library, we will start by building some very simple logistic regression models, with an aim at understanding the output, and build up to more complex models.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

First for 1 feature and 1 tag

For starters, let’s begin with the simplest possible question: do any of the TUNe+ features correspond directly to human tagging preferences for one of the MagnaTagATune tags? We set this up as a logistic regression with a single feature predicting a single tag. Try different features and tags until you find one with decent performance.

# choose the tag you would like to model (see annotations_df.columns for all tags)
my_favourite_tag = annotations_df['lol']

# choose the feature to predict your tag (change 0 to any other number in feature_df.columns)
my_favourite_feature = features_df[203]

# create train and test split
x_train_single, x_test_single, y_train_single, y_test_single = train_test_split(my_favourite_feature, my_favourite_tag, test_size=0.25)

# the clip_ids in the train and test splits
clips_train_single, clips_test_single = y_train_single.index.values, y_test_single.index.values

# when only using a single feature, we need to reshape the input arrays
x_train_single = x_train_single.values.reshape(-1, 1)
x_test_single = x_test_single.values.reshape(-1, 1)

single_feature_model = LogisticRegression(
    solver='liblinear',
    class_weight='balanced',
    random_state=0
    )
single_feature_model.fit(x_train_single, y_train_single)

LogisticRegression(class_weight='balanced', random_state=0, solver='liblinear')

We can look at the coefficients of our model to see how strong the relationship between our feature and our tag would be. Remember Gelman’s rule of thumb for interpreting logistic regression coefficients: if you divide them by 4, they give you an upper bound on how much the predicted probability of a clip being tagged a particular tag changes for every standard-deviation increase in the value of the feature. In this case, each standard-deviation increase reduced the probability of the tag by up to 15 percentage points. That sounds like a strong effect, but…

# model weight
single_feature_model.coef_

array([[-0.57181367]])

…the performance is mediocre:

# model accuracy
single_feature_model.score(x_test_single, y_test_single)

0.18839907192575406

Experiment with other tags and features until you find performance that you are happy with. Be smart about the tags you choose! Which ones do you think should be easy to predict based on an audio representation alone?

After you have a model that you are reasonably happy with, look at the clip-level predictions. When converting to logits, we need to beware that the first column of the predict_proba output is the probability that the tag is not used. If the model is a good one, the logits should be a good measure of the cognitive concept behind the tag.

Are they? Sort your predictions on the logit scale and listen to some of the highest- and lowest-ranking clips (and ideally some around zero and/or in the middle, too). Does your model seem to capture something associated with the tag with more granularity than a simple off–on?

log_prob_predictions_single = single_feature_model.predict_log_proba(x_test_single)
logit_predictions_single = pd.DataFrame(log_prob_predictions_single[:,1] - log_prob_predictions_single[:,0], columns=["logits"])
logit_predictions_single.index = clips_test_single
logit_predictions_single.index.name = "clip_id"
logit_predictions_single.sort_values(by="logits", ascending=False, inplace=True)
logit_predictions_single

	logits
clip_id
26494	0.097607
37360	0.097607
48908	0.097607
56370	0.097607
29399	0.097607
...	...
31491	-4.667621
51278	-4.713010
17245	-4.731373
20302	-4.836907
17239	-5.454134

6465 rows × 1 columns

my_clip = 26494
sound_file = annotations_df.loc[my_clip, 'mp3_path']
sound_audio = Audio(sound_file) 
display(sound_audio)

Now using all features

Most likely, you were not able to find a very good model using just one feature from the TUNe+ representation. Remember that it was trained to serve as an all-purpose representation, and not directly as a feature set for music tagging.

If TUNe+ is a good all-purpose representation, however, we should be able to get better predictions if we use the whole representation to predict a tag. Adapt the code below to explore some of the other tags that interested you in the previous section.

features_df.values.shape

(25860, 512)

# create train and test split
x_train_all, x_test_all, y_train_all, y_test_all = train_test_split(features_df.values, my_favourite_tag, test_size=0.25)

# the clip_ids in the train and test splits
clips_train_all, clips_test_all = y_train_all.index.values, y_test_all.index.values

# with this many features we need more than the default 100 iterations for the model to converge
all_feature_model = LogisticRegression(
    max_iter=500, 
    solver='liblinear',
    class_weight='balanced',
    random_state=0
    )
all_feature_model.fit(x_train_all, y_train_all)

LogisticRegression(class_weight='balanced', max_iter=500, random_state=0,
                   solver='liblinear')

Let’s look at the weights for each feature. Using Gelman’s rule of thumb, we can see that some features affect the probability of our example tag by as much as 48 percentage points! We can also see that many different features in the representation need to be used together in order to come to a measurement.

# weight for every feature
feature_weights = pd.DataFrame(all_feature_model.coef_.transpose(), columns=["weight"])
feature_weights.index.name = "feature_id"
feature_weights.sort_values(by="weight", inplace=True)
feature_weights

	weight
feature_id
477	-1.647431
97	-1.613888
119	-1.610214
176	-1.467999
199	-1.456123
...	...
339	1.544714
153	1.556762
190	1.650946
106	1.675281
238	2.143136

512 rows × 1 columns

# model accuracy
all_feature_model.score(x_test_all, y_test_all)

0.9848414539829853

Recompute the logit measures from this richer model and listen again to high-, low-, and mid-scoring clips. Is this model believable to the ear?

log_prob_predictions_all = all_feature_model.predict_log_proba(x_test_all)
logit_predictions_all = pd.DataFrame(log_prob_predictions_all[:,1] - log_prob_predictions_all[:,0], columns=["logits"])
logit_predictions_all.index = clips_test_all
logit_predictions_all.index.name = "clip_id"
logit_predictions_all.sort_values(by="logits", ascending=False, inplace=True)
logit_predictions_all

	logits
clip_id
23733	8.119262
6675	6.500905
32089	5.707097
12102	5.503760
27313	5.014884
...	...
33029	-48.287803
26004	-52.658945
52935	-56.124427
6887	-57.519651
52939	-57.678169

6465 rows × 1 columns

my_clip = 23733
sound_file = annotations_df.loc[my_clip, 'mp3_path']
sound_audio = Audio(sound_file) 
display(sound_audio)

Use L1 regularization / LASSO

The all-feature models obviously perform much better, but because they involve so many different features from the representation, we have not learned much about TUNe+.

LASSO is a popular, simple technique for feature selection in a regression context. Formally, it is a type of regularisation of a model, i.e., it introduce a penalty that pushes the feature weights back to zero. Only the most important features (in theory) will be able to overcome the penalty. In the case of LASSO, the penalty is the sum of the absolute value (L1 norm) of all of the weights; for these reason, another common name for LASSO in the literature is L1 regularisation. The specific advantage of LASSO over many other regularisation techniques is that it tends to push more weights not just close to zero, but actually all the way to zero.

See if L1 regularisation helps uncover whether you really need the entire TUNe+ representation to make good predictions of your chosen tag or tags.

# create train and test set, and now also a validation set to do some hyperparameter tuning on
x_train_lasso, x_test_lasso, y_train_lasso, y_test_lasso = train_test_split(features_df.values, my_favourite_tag, test_size=0.25)
x_train_lasso, x_val_lasso, y_train_lasso, y_val_lasso = train_test_split(x_train_lasso, y_train_lasso, test_size=0.25)

# the clip_ids in the train and test splits
clips_train_lasso, clips_test_lasso = y_train_lasso.index.values, y_test_lasso.index.values

all_feature_lasso_model = LogisticRegression(
    penalty='l1',
    solver='liblinear',
    class_weight='balanced',
    random_state=0
    )

To do LASSO properly, we want to find the optimal value for the penalty weight C. We will do a grid search for this. C is the inverse of regularization strength; smaller values specify stronger regularization (see the sklearn documentation for LogisticRegression).

cv = KFold(n_splits=2)
grid = {'C': np.arange(0.01, 1, 0.01)}
search = GridSearchCV(all_feature_lasso_model, grid, scoring='accuracy', cv=cv)
results = search.fit(x_val_lasso, y_val_lasso)
print('Mean absolute error: %.3f' % results.best_score_)
print('%s' % results.best_params_)

Mean absolute error: 0.998
{'C': 0.77}

# use the best C found in the grid search
all_feature_lasso_model = LogisticRegression(
    penalty='l1',
    C=results.best_params_['C'],
    solver='liblinear',
    class_weight='balanced',
    random_state=0
    )

all_feature_lasso_model.fit(x_val_lasso, y_val_lasso)

LogisticRegression(C=0.77, class_weight='balanced', penalty='l1',
                   random_state=0, solver='liblinear')

We can see that LASSO has indeed pushed our most important features to have even more extreme weights, although we are still far from a one-to-one mapping between the TUNe+ representation and tags. The performance cost of LASSO feature selection, however, is quite low.

# weight for every feature
feature_weights_lasso = pd.DataFrame(all_feature_lasso_model.coef_.transpose(), columns=["weight"])
feature_weights_lasso.index.name = "feature_id"
feature_weights_lasso.sort_values(by="weight", inplace=True)
feature_weights_lasso

	weight
feature_id
160	-0.804940
358	-0.764216
298	-0.678613
292	-0.674744
359	-0.543020
...	...
112	0.581912
124	0.609854
260	0.673610
266	0.941335
32	1.758986

512 rows × 1 columns

all_feature_lasso_model.score(x_test_lasso, y_test_lasso)

0.9953596287703016

Again, let’s look at our logit-scale measurement and listen. Notice that although our prediction performance is quite similar, at the measurement level, the ordering of clips has changed more substantially.

log_prob_predictions_lasso = all_feature_lasso_model.predict_log_proba(x_test_lasso)
logit_predictions_lasso = pd.DataFrame(log_prob_predictions_lasso[:,1] - log_prob_predictions_lasso[:,0], columns=["logits"])
logit_predictions_lasso.index = clips_test_lasso
logit_predictions_lasso.index.name = "clip_id"
logit_predictions_lasso.sort_values(by="logits", ascending=False, inplace=True)
logit_predictions_lasso

	logits
clip_id
43446	9.382512
27311	5.197331
836	4.982233
27309	4.557674
43193	3.971434
...	...
1143	-18.380548
31435	-18.479981
17562	-18.805916
7937	-19.644272
1141	-19.915417

6465 rows × 1 columns

my_clip = 43446
sound_file = annotations_df.loc[my_clip, 'mp3_path']
sound_audio = Audio(sound_file) 
display(sound_audio)

ASSIGNMENT

Explore the models above and (depending on your background) other more advanced models that use a log loss function. (TUNe+, for example, was evaluated not only with the simple logistic regression model above, but also with multi-layer perceptrons using the TUNe+ representation as input.)

Write a short report (250–500 words) that briefly summarises the model(s) you tried and describes your experience listening to the logit-scale predictions in more detail. Consider the following questions:

• Which MagnaTagATune tags are easy to predict from the TUNe+ representation. Which are hard? Do you have any intution as to why?

• If you examine your model weights across your models for different tags, are there any features within the TUNe+ representation that you think you could interpret? Do any of them, for example, seem to correspond to a particular genre or the presence of a particular voice/instrument?

• The TUNe+ representation performs very well when it comes to classification performance: nearly as well as fully supervised state-of-the-art models for predicting music tags. Does it peform as well in producing interpretable continuous logit scale? For example, if you chose the metal tag, do the highest values of your predictor correspond to the most metal-like clips, do values around 0 logits really feel like there is a 50–50 chance you’d tag the clip as metal, with a gradual transition in ‘heavy metal-ness’ between them?

• For what purposes would you advise musicologists to use the raw TUNe+ features and for what purposes would you advise them to use logit-scale tag predictors?